Uno stato termodinamico è identificato dalle sue coordinate termodinamiche, la pressione $P$, il volume $V$ e la temperatura $T$. Per passare da uno stato all’altro, è necessaria una variazione di queste coordinate, detta trasformazione termodinamica. È importante ricordare che:
- Se viene compiuta una variazione di volume $\Delta V$ a fronte della pressione $P$, epsressa da una forza di modulo $F$ applicata, come in figura, perpendicolarmente alla superficie $S$, viene compiuto un lavoro $\mathcal{L} = P \cdot \Delta V$. Ricordando la definizione di lavoro e di pressione, infatti, vale la relazione $$P \cdot \Delta V = \frac{F}{S} \cdot S\Delta \vec{s} =F \cdot \Delta x = \mathcal{L}$$

- Se varia la temperatura del sistema di una quantità $\Delta T$, viene scambiata una certa quantità di calore $\mathcal{Q} = C \Delta T$, dove $C$ è la capacità termica del sistema (ma attenzione: è possibile uno scambio di calore anche se la temperatura rimane invariata!)
Lavoro e calore, come provato dalle esperienze di Joule e dei padri della termodinamica, rappresentano entrambi degli scambi di energia tra sistemi fisici, o tra un sistema e l’ambiente. In generale, il lavoro o il calore scambiato durante una trasformazione termodinamica dipendono dalla trasformazione stessa: se da uno stato termodinamico $A$ passiamo ad un altro stato termodinamico $B$ attraverso una certa trasformazione $\Gamma_{A,B}$, il lavoro e il calore scambiati durante la trasformazione li indichiamo con $\mathcal{L}_{\Gamma_{A,B}}$ e $\mathcal{Q}_{\Gamma_{A,B}}$ rispettivamente. In generale, calcolare $\mathcal{L}_{\Gamma_{A,B}}$ e $\mathcal{Q}_{\Gamma_{A,B}}$ non è affatto facile: la trasformazione potrebbe essere qualsiasi cosa. Per questo motivo, almeno per i calcoli teorici, si studiano certe trasformazioni termodinamiche notevoli.
Tra le varie trasformazioni termodinamiche notevoli, ricordiamo le seguenti: isobara, caratterizzata da una pressione costante ($P = \text{ cost.}$); isocora, caratterizzata da un volume costante ($V = \text{ cost.}$); isoterma, caratterizzata da una tempreatura costante ($T = \text{ cost.}$); adiabatica, caratterizzata dall’assenza di scambi di calore ($\mathcal{Q} = 0$).
Fissiamo ora l’attenzione su due stati termodinamici $A$ e $B$, e cerchiamo, partendo da $A$, di raggiungere $B$ in diversi modi: ne facciamo di seguito qualche esempio. Supponiamo, per semplicità, che la pressione di $A$ sia maggiore di quella di $B$, mentre il volume occupato in $B$ sia maggiore del volume occupato in $A$; supponiamo anche che la temperatura in $A$ sia maggiore di quella in $B$. In figura sono rappresentate quattro diverse possibili trasformazioni, nel piano di Clapeyron, da $A$ a $B$:
- $\Gamma$: una trasformazione isocora da $A$ sino a raggiungere la stessa pressione di $B$, poi un’espansione isobara sino a raggiungere lo stesso volume di $B$.
- $\Theta$: un’espansione isobara sino a raggiungere lo stesso volume di $B$, e a seguire una riduzione di pressione isocora sino al livello di pressione di $B$.
- $\Psi$: un’espansione isoterma sino a raggiungere la stessa pressione di $B$, poi una compressione isobara sino a $B$.
- $\Lambda$: un’espansione adiabatica sino a raggiungere la stessa pressione di $B$, poi un’espansione isobara sino a $B$.

Durante i propri esperimenti, i vari scienziati che per primi esplorarono questo campo della fisica si accorsero che, sebbene lavoro e calore scambiati lungo una trasformazione termodinamica potevano variare a seconda della trasformazione stessa, una certa quantità rimaneva invariata per tutte le trasformazioni: la differenza tra calore e lavoro. Per questo motivo, si ipotizzò l’esistenza di una grandezza che non dipendesse dalla trasformazione impiegata per raggiungere $B$ da $A$, ma solo dagli stati iniziale e finale; coinvolgendo scambi di energia, era naturale interpretare questa quantità come una variazione di energia, la quale però non si manifestava macroscopicamente come energia cinetica o potenziale, e venne dunque chiamata energia interna. Indicando con $\mathcal{U}$ questa forma di energia, possiamo enunciare il primo principio della termodinamica con la formula $$ \Delta \mathcal{U} = \mathcal{Q} - \mathcal{L} \qquad \text{ lungo qualsiasi trasformazione } $$ dove, sia ben chiaro, il termine $\Delta \mathcal{U}$ è da intendersi come variazione di energia interna da uno stato termodinamico $A$ ad uno stato termodinamico $B$, cioè $ \Delta \mathcal{U} = \mathcal{U} (B) - \mathcal{U} (A) $, mentre $\mathcal{Q}$ e $\mathcal{L}$ sono da calcolarsi lungo una (stessa) trasformazione termodinamica che porta lo stato $A$ sino allo stato $B$.
Abbiamo visto come la grandezza $\mathcal{U}$ dipende unicamente dalle coordinate termodinamiche dello stato in cui viene calcolata: $\mathcal{U} = \mathcal{U}(V,P,T)$. Ma una serie di formulazioni teoriche ed esperimenti che vanno comunemente sotto il nome di teoria cinetica provarono che l’energia interna (più precisamente, variazioni di energia interna) altro non è che una manifestazione macroscopica, globale, dell’energia cinetica (più precisamente, variazioni di energia cinetica) posseduta dalle singole particelle che costituiscono il sistema. Quindi, l’energia interna dipende solo dalla temperatura: $$ \mathcal{U} = \mathcal{U} (T) $$
In quest’ottica, il primo principio della termodinamica costituisce una generalizzazione del principio della conservazione dell’energia meccanica: se per i sistemi conservativi classici era il lavoro $\mathcal{L}$ a non dipendere dal cammino percorso, ora è la quantità $ \mathcal{Q} - \mathcal{L}$ a non dipendere dalla trasformazione seguita.
Grazie al primo principio della termodinamica, possiamo rendere conto di alcuni fenomeni.
Premettiamo che, nei grafici di trasformazioni termodinamiche tracciati nel piano di Clapeyron, è uso indicare con delle frecce il lavoro ed il calore scambiati durante una determinata trasformazione. Queste frecce attraversano la curva che rappresenta la trasformazione, e sono prevalentemente verticali per i calori e orizzontali per i lavori.
Come primo esempio, consideriamo una trasformazione isocora, in cui il volume non cambia. Non essendoci variazione di volume, il lavoro sarà nullo: $\mathcal{L} = 0$; di conseguenza, per il primo principio della termodinamica, la variazione di energia interna sarà interamente causata dallo scambio di calore: $ \mathcal{U} = \mathcal{Q} $. Dalla definizione di calore specifico, sappiamo che il calore scambiato lungo una trasformazione isocora è, per unità di massa, $ \mathcal{Q} = c_V \Delta T $ (ove $c_V$ è il calore specifico a volume costante).
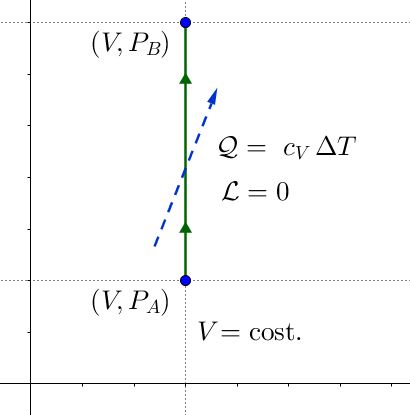
Di contro, consideriamo una trasformazione adiabatica: adesso è il calore a non essere scambiato, ossia $\mathcal{Q} = 0$; per il primo principio sarà quindi $\Delta \mathcal{U} = -\mathcal{L}$. Questo cambiamento di segno è coerente con l’esperienza: come ha mostrato Joule, fornendo lavoro ad un sistema ($\mathcal{L} < 0$) è possibile innalzarne la temperatura ($\Delta T > 0$), e quindi, tenendo presente la teoria cinetica, anche l’energia interna viene incrementata ($\Delta \mathcal{U} > 0$).

Per quanto riguarda una trasformazione isobara, a pressione costante, il lavoro è, come fatto notare in precedenza, $ \mathcal{L} = P \Delta V$, dove $P$ è la pressione a cui avviene la trasformazione; il calore scambiato, sempre dalla definizione di calore specifico, risulta essere, per unità di massa, $ \mathcal{Q} = c_P \Delta T $. Si ha quindi una variazione di energia interna pari a $\Delta \mathcal{U} = \mathcal{Q} - \mathcal{L} = c_P \Delta T - P \Delta V$.

Infine, consideriamo una trasformazione isoterma (che avviene ad una temperatura, fissa, $T$) che da uno stato $A$, caratterizzato da pressione $P_A$ e volume $V_A$, porta ad uno stato $B$, dotato di pressione $P_B$ e volume $V_B$. Supponiamo che $V_B > V_A$ di modo che $P_B < P_A$.

Siccome la temperatura non cambia, in base a quanto detto sull’energia interna è $\Delta \mathcal{U} = 0$. Per l’espressione del primo principio della termodinamica, $\mathcal{L} = \mathcal{Q}$, ovvero tutto il lavoro $ \mathcal{L}$ che il sistema effettua per incrementare il proprio volume da $V_A$ a $V_B$ si tramuta in calore, $\mathcal{Q}$, che va fornito in qualche modo al sistema (ad esempio, ponendolo a contatto termico con una sorgente esterna). Quindi, come accennato all’inizio, è possibile uno scambio di calore a temperatura costante! Notiamo che il lavoro (essendo $V_B > V_A$) è positivo, e di conseguenza anche il calore: il sistema compie lavoro, espandendosi, ma è necessario fornire calore.
Se volessimo cambiare il verso della trasformazione, ossia se volessimo comprimere il sistema dal volume $V_B$ a quello minore $V_A$, il lavoro risulterebbe negativo: dovremmo compiere un lavoro sul sistema; per il primo principio, quest’ultimo fornirebbe all’ambiente una quantità di calore esattamente uguale al lavoro subito.

Chiamiamo “macchina termica” un sistema termodinamico in grado di scambiare calore e lavoro con l’ambiente o con altri sistemi termodinamici. Il primo principio della termodinamica sancisce, tra le altre cose, che le macchine termiche altro non fanno se non trasformare calore in lavoro, in porzioni più o meno ampie, ma sempre di modo che la differenza tra queste due grandezze rimanga costante la differenza. In pratica, non è possibile generare energia dal nulla (o distruggere energia) ma è sempre necessario fornire o calore o lavoro, di modo che la differenza $\mathcal{Q} - \mathcal{L}$ sia positiva (rispettivamente, negativa).

Tuttavia il primo principio non vieta di pensare alla situazione seguente. Immaginiamo di costruire una macchina termica che converta completamente il calore fornitole in lavoro: ad esempio, una macchina in grado di compiere una trasformazione isoterma da uno stato a pressione maggiore a uno stato a pressione minore, come evidenziato nell’esempio precedente. Ora supponiamo di costruire un’altra macchina termica, che converta completamente il lavoro fornitole in calore: ad esempio, una macchina in grado di compiere una trasformazione isoterma da uno stato a pressione minore a uno stato a temperatura maggiore. Infine, pensiamo di collegare queste due macchine: a fronte di calore fornitole $\mathcal{Q}$, la prima macchina lo trasforma in lavoro $\mathcal{L}$ e fornisce questo lavoro alla seconda macchina; questa, dal canto suo, trasforma il lavoro fornitole $\mathcal{L}$ di nuovo in calore $\mathcal{Q}$, che cede alla prima macchina, mettendo nuovamente in moto il processo. Un processo fisico che, una volta messo in moto, è in grado di autoalimentarsi, senza bisogno di intervento esterno, si dice moto perpetuo: abbiamo appena costruito il moto perpetuo termodinamico!

Anche nei primi stadi dello sviluppo di questa disciplina si seguì un ragionamento analogo, e si cercò di costruire macchine termiche in grado di trasformare completamente calore in lavoro o lavoro in calore. Tutti i tentativi fallirono: purtroppo, nessun tentativo può riuscire, poiché sussiste infatti il secondo principio della termodinamica.