Il teorema degli incrementi finiti di Cauchy è uno dei teoremi classici dell’Analisi Matematica, la cui importanza è giustificata dal fatto che il teorema di Lagrange risulta esserne una conseguenza banale. In questa lezione daremo l’enunciato e la dimostrazione del teorema, e poi ne forniremo una intuizione geometrica con un esempio mirato.
TEOREMA (di Cauchy, o degli incrementi finiti): Prendiamo due funzioni $f(x)$ e $g(x)$ continue in un intervallo $[a, b]$ e derivabili sull’intervallo $(a, b)$. Allora esiste un punto $c \in (a, b)$ tale per cui valga la relazione $$f’(c) \cdot \left ( g(b)-g(a) \right ) = g’(c) \cdot \left ( f(b) - f(a) \right )$$Se inoltre valgono le condizioni $g’(c) \neq 0$ e $g(b) \neq g(a)$ allora questa relazione può essere riscritta così: $$\frac{f’(c)}{g’(c)} = \frac{f(b) - f(a)}{g(b)-g(a)}$$Dimostrazione. Dividiamo la dimostrazione in due casi.
1. Supponiamo che $g(a) = g(b)$. Allora la funzione $g$ soddisfa le ipotesi del teorema di Rolle, e quindi esiste un $c \in (a, b)$ tale per cui $g’(c) = 0$. A questo punto, se scegliamo proprio questo $c$, la relazione $f’(c) \cdot (g(b)-g(a)) = g’(c) \cdot (f(b) - f(a))$ diventa equivalente all’uguaglianza $0=0$, e quindi il teorema è banalmente vero.
2. Supponiamo invece che $g(a) \neq g(b)$. Allora possiamo definire senza problemi il numero $$R = \frac{f(b) - f(a)}{g(b)-g(a)}$$Consideriamo la funzione ausiliaria $h(x)$ definita in questo modo: $$h(x) = f(x) - Rg(x)$$Questa funzione rispetta le ipotesi del teorema di Rolle:
- per definizione, $h(x)$ è combinazione lineare di $f(x)$ e $g(x)$, che sono due funzioni che per ipotesi sono continue in $[a, b]$ e derivabili in $(a, b)$; quindi anche $h(x)$ rispetta tali condizioni.
- abbiamo che ##KATEX##\begin{aligned} h(a) & = f(a) - \frac{f(b) - f(a)}{g(b)-g(a)}g(a) = \frac{f(a) \left ( g(b)-g(a) \right ) - g(a) \left ( f(b) - f(a) \right )}{g(b)-g(a)} = \\ & = \frac{g(b)f(a) - g(a)f(b)}{g(b)-g(a)} \end{aligned}##KATEX## ma anche ##KATEX##\begin{aligned} h(b) & = f(b) - \frac{f(b) - f(a)}{g(b)-g(a)}g(b) = \frac{f(b) \left ( g(b)-g(a) \right ) - g(b) \left ( f(b) - f(a) \right )}{g(b)-g(a)} = \\ & = \frac{-f(b)g(a) + f(a)g(b)}{g(b)-g(a)} \end{aligned}##KATEX##Confrontando le due espressioni vediamo quindi che $h(a) = h(b)$.
Il teorema di Rolle, allora, ci dice che esiste un valore $c \in (a, b)$ tale per cui $h’(c) = 0$. Visto che $$h’(x) = \left ( f(x) - Rg(x) \right )’ = f’(x) - Rg’(x),$$allora otteniamo: $$h’(c) = 0 \quad \Leftrightarrow \quad f’(c) = Rg’(c) \quad \Leftrightarrow \quad f’(c) \left ( g(b)-g(a) \right ) = g’(c) \left ( f(b) - f(a) \right )$$L’ultima relazione è proprio quella che volevamo dimostrare.
Il teorema di Cauchy può essere visto come una generalizzazione del teorema di Lagrange. Se infatti consideriamo una funzione $f(x)$ che rispetti le ipotesi del teorema e poniamo invece $g(x) = x$ (che è sempre continua in un qualsiasi intervallo $[a, b]$ e derivabile in $(a, b)$) allora abbiamo che $g’(c) = 1$ e $g(b) = b \neq a = g(a)$ (stiamo escludendo il caso limite in cui l’intervallo sia ridotto a un solo punto $a=b$, privo di interesse). Possiamo allora utilizzare la seconda formulazione del teorema ottenendo: $$\frac{f’(c)}{g’(c)} = \frac{f(b) - f(a)}{g(b)-g(a)} \qquad \Rightarrow \qquad f’(c) = \frac{f(b) - f(a)}{b-a}$$che è proprio l’enunciato del teorema di Lagrange applicato alla funzione $f(x)$.
Interpretazione geometrica del teorema di Cauchy: il caso della semicirconferenza
Prendiamo la funzione $$s(x) : y = \sqrt{1 - x^2}$$Questa funzione è sempre positiva, ed è definita quando $x \in [-1, 1]$. Essa descrive la semicirconferenza di raggio $1$ centrata nell’origine degli assi: infatti, basta elevare al quadrato entrambi i membri per ottenere l’equazione della circonferenza $x^2 + y^2 = 1$, tenendo però presente che possiamo considerare su di essa solo i punti con $y > 0$.
Preso un punto $P$ della semicirconferenza, si può vedere abbastanza facilmente che le sue coordinate polari sono date da $(1, t)$ dove $t$ è l’angolo compreso tra l’asse $x$ e il segmento $OP$; dato che stiamo considerando una semicirconferenza, l’angolo $t$ varierà nell’intervallo $[0, \pi]$. Se vogliamo esprimere $P$ in coordinate cartesiane, otteniamo le seguenti relazioni: $$\begin{cases} x = 1 \cdot \cos (t) = \cos (t) \\ y = 1 \cdot \sin (t) = \sin (t) \end{cases}$$In sostanza possiamo descrivere la semicirconferenza come curva parametrica (che è un modo di chiamare una funzione di più variabili da $\mathbb{R}$ a $\mathbb{R}^n$) tramite le funzioni ##KATEX##\begin{aligned} g(t) & := \cos (t) \\ f(t) & := \sin (t) \end{aligned}##KATEX## con $t$ che varia tra $[0, \pi]$. In questo modo siamo sicuri che ciascun punto $P$ che giace sulla semicirconferenza avrà coordinate $\left ( \cos (t), \sin (t) \right ) $ per un opportuno $t \in [0, \pi]$.
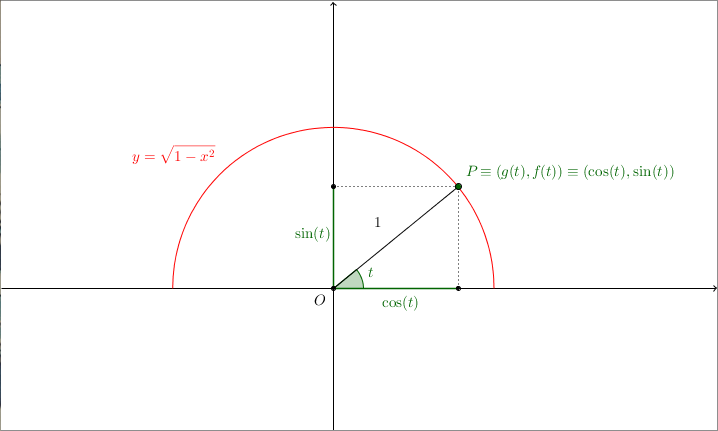
Scegliamo due numeri $a, b \in [0, \pi]$. Le funzioni $f(t) = \sin (t)$, $g(t) = \cos (t)$ sono continue in $[a, b]$ e derivabili nell’intervallo $(a, b)$, e quindi possiamo applicare il teorema di Cauchy: esiste dunque un certo $c \in (a, b)$, che per semplicità supporremo soddisfare la relazione $g’(c) \neq 0$, per cui vale la relazione ##KATEX##\begin{equation} \frac{f’(c)}{g’(c)} = \frac{f(b) - f(a)}{g(b)-g(a)} \end{equation}##KATEX##Come possiamo interpretare questo fatto?
Facciamo le seguenti osservazioni.
- Calcoliamo la derivata della funzione $s$ che descrive la semicirconferenza: $$s’(x) = \left ( \sqrt{1 - x^2} \right )’ = \frac{1}{2 \sqrt{1-x^2}} \cdot \left ( -2x \right ) = \frac{-x}{\sqrt{1-x^2}}$$Dato che $x = \cos (t)$, abbiamo: $$\frac{-x}{\sqrt{1-x^2}} = \frac{-\cos(t)}{\sqrt{1 - \cos^2(t)}} = \frac{-\cos(t)}{\sin(t)}.$$Siccome $(\sin (t) )’ = - \cos(t)$ e $(\cos(t))’=\sin (t)$, vale anche la relazione: $$\frac{-\cos(t)}{\sin(t)} = \frac{( \sin(t) )’}{ ( \cos(t))’} = \frac{f’(t)}{g’(t)}.$$In sostanza abbiamo ottenuto un modo di esprimere la derivata della funzione $s$ in termini della variabile $t$: $$s’ = \frac{f’(t)}{g’(t)}.$$Questo ci dice, quindi, che il coefficiente angolare della retta $r$ tangente alla semicirconferenza nel punto $C$ (corrispondente a $t=c$) è proprio $m_r = \frac{f’(c)}{g’(c)}$, che è il primo membro della relazione ottenuta con il teorema di Cauchy.
- Consideriamo i punti sulla semicirconferenza corrispondenti ad $a$ e $b$: $A \equiv \left ( \cos (a), \sin (a) \right )$ e $ B \equiv \left ( \cos (b), \sin (b) \right )$. A partire da questi punti, è sempre ben definito il coefficiente angolare della retta passante per $A$ e $B$: $$m_{AB} = \frac{\sin(b) - \sin(a)}{\cos(b) - \cos(a)} = \frac{f(b) - f(a)}{g(b) - g(a)}$$Questo è il secondo membro della relazione espressa dal teorema.
In sostanza il teorema di Cauchy applicato alla funzione che descrive la semicirconferenza si riconduce a questa osservazione:
Data una qualsiasi corda $AB$ di una semicirconferenza, esiste sempre una retta tangente a essa che abbia lo stesso coefficiente angolare della retta su cui giace $AB$.
