Come i pianeti si muovano nel cielo è una questione che affascina l’uomo sin dall’antichità. Molti modelli ne sono stati presentati nel corso della storia. Secondo Aristotele (e Tolomeo), il moto dei pianeti e degli altri satelliti (come la la Luna) avveniva in traiettoria circolare attorno alla Terra, posta al centro dell’universo: i corpi celesti, infatti, erano ritenuti perfetti, ed era quindi conseguenza che le loro orbite fossero descritte da cerchi concentrici, forme perfette, infinite, prive di inizio e fine, immutabili; il moto di ciò che avveniva sulla terra, caduco e corruttibile, obbediva invece a leggi differenti.
Lo scienziato polacco Copernico propose un modello dell’universo in cui al centro era situato il Sole, e attorno ad esso ruotassero, sempre in orbite circolari concentriche, gli altri pianeti, compresa la terra: questo rendeva conto di alcuni fenomeni che si riscontrano sul nostro pianeta, e di molte osservazioni fatte dallo stesso Copernico; tuttavia, anche il modello copernicano non riusciva a render conto di molti altri dati raccolti dalle osservazioni astronomiche.
All’inizio del 1600, lo scienziato tedesco Johannes von Kepler (latinizzato in Giovanni Keplero) formulò tre leggi, sulla base delle osservazioni del suo maestro danese Tycho Brahe, che prevedevano perfettamente (e lo fanno tutt’ora) il moto dei pianeti all’interno del sistema solare.
Va precisato che queste sono leggi sperimentali, ovvero prevedono correttamente il comportamento dei corpi celesti entro il sistema solare, in accordo con i dati sperimentali, ma non ne spiegano le cause.
Prima Legge
L’enunciato della prima legge di Keplero riguarda la forma delle orbite:
- “Le orbite descritte dai pianeti attorno al Sole sono ellissi di cui il sole occupa uno dei fuochi”
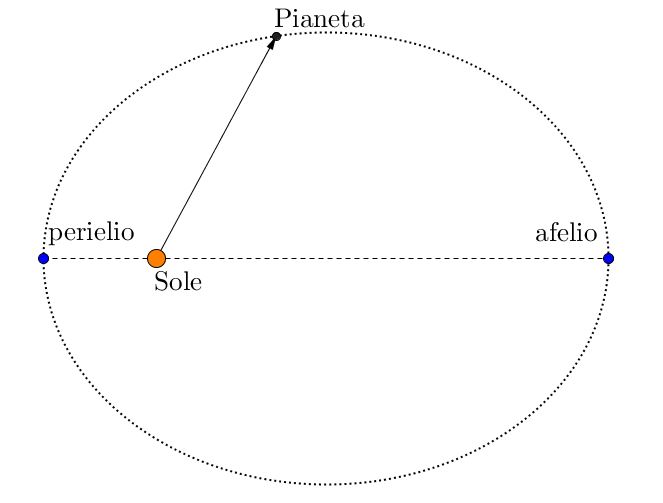
Ricordiamo che un ellisse è una figura piana, definita come il luogo dei punti del piano la cui somma delle distanze da due punti fissi, detti fuochi, è costante. Con riferimento alla figura sottostante, indichiamo con $a$ la lunghezza del semiasse maggiore dell’ellisse, con $b$ la lunghezza del semiasse minore. La distanza dei due fuochi dal centro dell’ellisse sarà $c$, calcolato tramite il teorema di pitagora: $c = \sqrt{a^2 - b^2}$.

Per la prima legge di Keplero, il Sole occupa la posizione di uno dei due fuochi, mentre l’altro fuoco è lasciato libero; il punto in cui un pianeta orbitante attorno al Sole gli è più vicino si chiama perielio, mentre il punto dell’orbita in cui il pianeta è più distante è detto afelio (sono entrambe parole che derivano dal greco antico: infatti, helios vuol dire “sole”, perì significa “accanto”, e apò significa “lontano”).
La prima legge, oltre a regolare la forma dell’orbita, fornisce anche un’informazione in più: essendo un ellisse una figura piana, le orbite avvengono su un unico piano.
Seconda Legge
La seconda legge di Keplero regola la velocità orbitale di un pianeta: essa non è costante, come in un moto circolare uniforme; la sua magnitudine è infatti determinata dalla sua posizione. L’enunciato della seconda legge è il seguente:
- “il raggio vettore che unisce il sole al pianeta orbitante descrive aree uguali in tempi uguali”
Per “raggio vettore” si intende il vettore che possiede per direzione la retta passante per il punto che indica la posizione del pianeta e il punto che indica la posizione del Sole, per verso quello che dal Sole punta al pianeta e per modulo la distanza consistente tra il pianeta stesso e il Sole: in parole povere, una freccia che punta dal Sole al pianeta orbitante. Man mano che il pianeta compie la sua orbita, questo vettore descrive un’area, una specie di “settore ellittico”.
Supponiamo che trascorra un intervallo di tempo di durata $\Delta t$, e che in questo intervallo di tempo il pianeta venga a portarsi dalla posizione iniziale $x_1$ a quella finale $x_2$, compiendo dunque uno spostamento $\Delta \vec{x} = x_2 - x_1$. La seconda legge asserisce che, fermo restando l’intervallo di tempo $\Delta t$, l’area di questo settore ellittico rimane sempre la stessa, indipendentemente dalla posizione di partenza $x_1$ del pianeta:

La velocità del pianeta orbitante non è costante: come si vede dalle immagini, più il pianeta si trova vicino al sole, minore è il raggio, e, di conseguenza, maggiore deve essere la velocità con cui il pianeta si muove. Se la velocità fosse costante, le aree descritte dal raggio pianeta-sole in intervalli di tempo uguali sarebbero differenti.

Possiamo enunciare la seconda legge di Keplero con una formula matematica. Immaginiamo che un pianeta orbiti attorno al Sole per un intervallo di tempo di durata $\Delta t$. Se chiamiamo $\Delta \mathcal{S}$ l’area descritta dal raggio vettore in questo periodo di tempo, la seconda legge di Keplero ci indica che questa quantità rimane costante durante il moto: possiamo dunque asserire che la velocità areolare, ossia il rapporto tra l’area spazzata dal raggio vettore $\Delta \mathcal{S}$ e la durata $\Delta t$ dell’intervallo di tempo impiegato a descriverla, è costante:$$ \frac{\Delta \mathcal{S}} {\Delta t } = \text{ costante}$$
Terza Legge
La terza e ultima legge di Keplero concerne il periodo impiegato da un pianeta a compiere un’orbita completa. Essa stabilisce che:
- “il rapporto tra il cubo del semiasse maggiore dell’orbita e il quadrato del periodo di rivoluzione è lo stesso per tutti i pianeti”
Abbiamo introdotto il periodo $T$ per il moto armonico e il moto circolare; il periodo non è una grandezza tipica solo di quei moti, ma caratterizza un'intera categoria di moti, detti appunto moti periodici: un certo punto materiale si muove di moto periodico se, dopo un certo lasso di tempo, esso ritorna in una posizione precedentemente raggiunta con la medesima velocità. Si dice periodo di un moto periodico il più piccolo intervallo di tempo $T$ per cui questo fenomeno si verifica.
In base alla prima e alla seconda legge di Keplero, il moto dei pianeti nel sistema solare è un moto periodico: essendo l’orbita ellittica (che è una curva chiusa), il pianeta tornerà sicuramente su posizioni occupate precedentemente; inoltre, data la seconda legge di Keplero, la velocità orbitale posseduta da un pianeta sarà determinata dalla sua posizione nell’orbita, e quindi, passando per lo stesso punto, anche la velocità sarà la medesima. Ne concludiamo che il moto dei pianeti nel sistema solare è periodico.
Per un’orbita chiusa, il periodo è semplicemente la durata di “un giro completo”. Se chiamiamo $T$ il periodo del moto di un pianeta, e $a$ la misura del semiasse maggiore della sua orbita, la terza legge di Keplero può essere riassunta dalla seguente formula matematica:$$ \frac{ a^3 }{ T^2 } = \text{ costante}$$La costante venne determinata da Keplero in persona, e per questo viene a volte indicata con la lettera $K$ e prende il nome di “costante di Keplero”. Questa costante dipende dal corpo celeste attorno a cui viene calcolata l’orbita.
Le leggi di Keplero, pur descrivendo perfettamente tutti i fenomeni celesti che si possono osservare nel nostro sistema solare, non spiegano le cause di questi stessi fenomeni: come accennato in principio, esse sono infatti leggi sperimentali, le quali prevedono esattamente, con calcoli matematici, i risultati delle osservazioni scientifiche. Il motivo per il quale il sistema solare, e in generale un sistema di corpi orbitanti attorno ad uno molto più massivo, aderisca per filo e per segno alle leggi di Keplero venne illustrato da Isaac Newton con la teoria della gravitazione universale: mediante lo sviluppo di nuove discipline matematiche, egli riuscì a mostrare la validità delle leggi di Keplero, assumendo come punto di partenza le leggi della dinamica e la legge di gravitazione universale.
In particolare, il lavoro di Newton consistette dei seguenti punti:
- Per la forza gravitazionale, il momento meccanico $\vec{M}$ risulta nullo, poichè la forza è sempre diretta come il braccio: di conseguenza, il momento angolare $\vec{L}$ si conserva. Si può dimostrare come il modulo del momento angolare, in questo caso, sia il doppio della quantità $\frac{\Delta \mathcal{S}}{ \Delta t}$ descritta precedentemente: dunque, anche quest’ultima si conserva. Conservandosi come vettore, il momento angolare definisce anche il piano su cui avviene il moto del pianeta.

- Sfruttando tecniche matematiche da lui stesso inventate (che oggi vanno sotto il nome di calcolo infinitesimale), Newton riuscì a ricondursi al calcolo della forma dell’orbita, giungendo ai risultati previsti da Keplero: le orbite, sotto precise ipotesi, risultavano ellittiche.

- Riconducendo la misura del semiasse maggiore ad altre quantità (precisamente, all’energia cinetica posseduta dal corpo celeste, al suo momento angolare, alla massa del pianeta in questione e alla costante di gravitazione universale), Newton dimostrò che il quadrato del periodo di rivoluzione di un pianeta doveva essere proporzionale al cubo del semiasse maggiore della sua orbita, in accordo con le leggi di Keplero.