Data una circonferenza $\mathcal{C}$ e un punto $P$ come si trova una tangente a $\mathcal{C}$ che passi per $P$? Si tratta di un problema classico della geometria analitica che può essere affrontato in diversi modi. Uno dei più comodi, almeno in alcuni casi, fa uso della retta polare di $P$ rispetto a $\mathcal{C}$.
Per cominciare vediamo come ottenere la retta polare, e poi vediamo come utilizzarla per il problema delle tangenti. Si tratta di una procedura piuttosto semplice. Supponiamo di avere una circonferenza $\mathcal{C}$ ed un punto $P$ di coordinate $(x_0;y_0)$:
- Si parte dall’equazione della circonferenza $\mathcal{C}$ espressa in forma normale $$ x^2 + y^2 + ax + by + c = 0$$
- Si effettuano le seguenti sostituzioni nell’equazione di $\mathcal{C}$: $$x^2 \to x \cdot x_0 \qquad y^2 \to y \cdot y_0$$ $$x \to \frac{x+x_0}{2}\qquad y \to\frac{y+y_0}{2}$$
- Si ottiene così l’equazione della retta polare di $P$ rispetto a $\mathcal{C}$: $$x\cdot x_0 + y\cdot y_0 + a \frac{x+x_0}{2} + b \frac{y+y_0}{2}+c=0 $$
Dal momento che $x_0$ e $y_0$ sono entrambi valori costanti e non variabili, il risultato ottenuto è un’equazione di primo grado in $x$ e $y$ e quindi rappresenta effettivamente una retta.
La procedura seguita per ottenere la retta polare va sotto il nome di metodo dello sdoppiamento perché ogni variabile viene sdoppiata: attraverso un prodotto se la variabile di partenza era elevata al quadrato o attraverso una media aritmetica se in origine era lineare.
A seconda della posizione del punto rispetto alla circonferenza possiamo distinguere tre casi:
- Punto interno alla circonferenza: la retta polare è esterna alla circonferenza. Nella figura la retta $q$ è la polare del punto $Q$ rispetto alla circonferenza centrata in $O$.
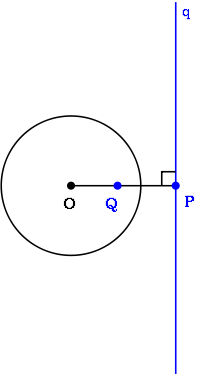
- Punto appartenente alla circonferenza: la retta polare è tangente alla circonferenza. Questo è il caso in cui l’uso della retta polare semplifica molto i calcoli: per trovare la tangente a $\mathcal{C}$ passante per $P$ è infatti sufficiente applicare il metodo degli sdoppiamenti.
- Punto esterno alla circonferenza: la retta polare è secante la circonferenza. Nella figura $p$ è la retta polare del punto $P$ rispetto alla circonferenza $\mathcal{C}$ e interseca $\mathcal{C}$ in due punti, $P_1$ e $P_2$.

E’ importante notare che la retta passante per $P$ e $P_1$ è tangente a $\mathcal{C}$ e quindi costituisce una soluzione al problema che ci siamo posti all’inizio. Lo stesso si può dire della retta che passa per $P$ e $P_2$. Possiamo quindi affermare che la retta polare di un punto $P$ esterno ad una circonferenza $\mathcal{C}$ congiunge i due punti di tangenza $P_1$ e $P_2$.
Per trovare le rette passanti per un punto esterno $P$ e tangenti a $C$ si opera allora in tre passaggi. Vediamoli nel dettaglio facendo riferimento a un esempio in cui la circonferenza ha equazione $x^2+y^2-2x=0$ e il punto esterno ha coordinate $P \equiv (1; \frac{5}{4})$
- Si calcola la retta polare col metodo degli sdoppiamenti. Nel nostro caso: $x\cdot 1+y\cdot \frac{5}{4}-2\frac{x+1}{2}=0\quad\to\quad\frac{5}{4} y = 1$, da cui ricaviamo la retta polare (orizzontale nel nostro caso) $q$: $y=\frac{4}{5}$
- Si calcolano le intersezioni $P_1$ e $P_2$ della retta polare $q$ con la circonferenza $\mathcal{C}$, mettendo a sistema le rispettive equazioni. Nel nostro caso: il sistema di secondo grado formato dall'equazione della retta e da quella della circonferenza $$\begin{cases} x^2+y^2-2x=0 \\ y=\frac{4}{5}\end{cases} $$ in questo caso si risolve con una semplice sostituzione. Si ottiene un'equazione di secondo grado $$ x^2-2x+\frac{16}{25}=0 $$ le cui soluzioni si ottengono con la formula risolutiva ridotta: $$ x_{1,2} = 1\pm\sqrt{1-\frac{16}{25}} = 1\pm\sqrt{\frac{9}{25}}=1 \pm \frac{3}{5}$$ Quindi i due punti di intersezione sono $P_1 \equiv \left(\frac{2}{5},\frac{4}{5}\right)$ e $P_2 \equiv \left(\frac{8}{5}, \frac{4}{5}\right)$.
- Si calcolano le equazioni delle due rette passante per le due coppie di punti $P \ P_1$ e $ P \ P_2$. Nel nostro caso: la prima tangente di equazione $ y = m_1 x+q_1 $ si ottiene imponendo il passaggio per $P$ e $P_1$, cioè sostituendo a $x$ e $y$ le relative coordinate di ciascun punto e mettendo a sistema le equazioni in $m_1$ e $q_1$ così ottenute: $$\begin{cases} \frac{5}{4} = m_1 \cdot 1 + q_1 \\ \frac{4}{5} = m_1 \cdot \frac{2}{5} + q_1\end{cases}$$ Risolvendo il sistema ricaviamo i valori $m_1 = \frac{3}{4}$ e $q_1 = \frac{1}{2}$ che corrispondono alla retta $r_1$: $ y = \frac{3}{4} x + \frac{1}{2}$. Con passaggi analoghi si ottiene la seconda tangente $r_2$: $y = -\frac{3}{4}x + 2$.
Crediti immagine: WillowW http://en.wikipedia.org/w/index.php?title=File:Pole_and_polar.svg&page=1