Un risultato fondamentale nella descrizione dei fenomeni elettrostatici è costituito dal Teorema di Gauss, applicato al campo elettrostatico. Esso costituisce una parte fondamentale delle leggi che permettono di descrivere completamente, almeno nella meccanica classica, il comportamento di corpi carichi sottoposti a interazioni elettro-magnetiche, relazioni matematiche condensate nelle equazioni di Maxwell.
Solo per enunciare il teorema di Gauss, tuttavia, abbiamo bisogno di comprendere due concetti della fisica: il concetto di campo vettoriale, nella fattispecie di campo elettrico, e il concetto di flusso di un campo vettoriale attraverso una superficie.
Un campo vettoriale è una legge che assegna a ciascun punto (nello spazio) un vettore. Ricordiamo che un vettore è un’entità matematica caratterizzata da quattro attributi: modulo (la sua lunghezza), direzione (la retta su cui giace il vettore), verso (il verso in cui punta il vettore sulla propria direzione) e punto di applicazione (il punto dal quale ha origine il vettore). In parole povere, un vettore è una “freccia” che scaturisce da un punto nello spazio, e se in ogni punto dello spazio abbiamo una “freccia” che sbuca, abbiamo un campo vettoriale.
Il campo vettoriale con cui lavoreremo è il campo elettrico: ricordiamo che una carica elettrica $q$ genera, in un punto $P$ posto a distanza $r$ da esso, un vettore $$ \vec{E}_q (r) = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \vec{u}_r $$dove il vettore $\vec{u}_r$ è un vettore di modulo $1$ (detto anche versore) che parte da dove è posto $P$ e punta da $q$ verso $P$:

Se invece di avere una sola carica ne abbiamo molte, ad esempio $n$, il campo elettrico risultante sarà la somma vettoriale dei campi elettrici generati dalle singole cariche: $$ \vec{E}_{TOT} = \sum_{i = 1}^n \vec{E}_i $$
Adesso supponiamo di avere un campo vettoriale $\vec{V}$. Per semplicità, consideriamo un campo uniforme, cioè sempre uguale in modulo ($V$), direzione e verso. Ora prendiamo una superficie $\mathcal{S}$ di area $S$, e supponiamo, sempre per semplicità, che essa sia perpendicolare alle linee di campo del campo $\vec{V}$. In questo particolarissimo caso, definiamo il flusso del campo $\vec{V}$ attraverso la superficie $\mathcal{S}$ come $$ \Phi_{\mathcal{S}} \left(\vec{V}\right) = V\ S $$Se $\mathcal{S}$ non è perpendicolare alle linee di campo, dobbiamo rendere conto, nel calcolo del flusso, dell’angolo con il quale le linee attraversano la superficie: chiamato $\vec{n}$ il versore perpendicolare alla superficie $\mathcal{S}$, che forma un angolo $\alpha$ con il vettore $\vec{V}$, poniamo $$ \Phi_{\mathcal{S}} (\vec{V}) = \vec{V} \cdot S\vec{n} = V S \cos(\alpha)$$

In generale la situazione è assai più complicata: il versore normale alla superficie $\mathcal{S}$ cambia di punto in punto, così come il vettore $\vec{V}$: questo porta a calcoli piuttosto complessi. Adottiamo però subito una convenzione: nel caso in cui la superficie $\mathcal{S}$ racchiuda un volume finito, ossia nel caso in cui sia una superficie chiusa, il verso in cui punta il versore $\vec{n}$ è quello uscente dalla superficie. Si parlerà quindi di flusso uscente:

Dalla definizione si evince che il flusso è massimo quando la superficie è perpendicolare alle linee di campo, ossia quando il versore normale e il campo vettoriale sono paralleli ($\alpha = 0 \vee \alpha =180^\circ$), mentre è nullo quando le linee di campo sono parallele, radenti alla superficie, ossia quando il versore normale e il campo vettoriale formano un angolo retto ($\alpha = 90^\circ \vee \alpha =270^\circ$): questo è esattamente quello che possiamo verificare nella pratica, ad esempio infilando la mano in un corso d’acqua e variandone l’inclinazione.
Ora siamo pronti per enunciare il teorema di Gauss, che ci permette di calcolare il flusso del campo elettrico generato da una certa distribuzione di carica elettrica attraverso una superficie senza svolgere i calcoli prescritti dalla definizione di flusso.
Data una superficie chiusa $\mathcal{S}$ contenente un numero qualunque di cariche elettriche (positive o negative), il flusso del campo elettrico (generato dalle cariche) attraverso tale superficie è uguale al rapporto tra la somma algebrica dei valori delle cariche contenute entro la superficie chiusa e la costante dielettrica $\varepsilon$ del mezzo in cui si trovano le cariche ($\varepsilon_0$ nel vuoto): $$ \Phi_{\mathcal{S}} (\vec{E}) = \frac{\sum q_{\text{int}}}{\varepsilon} $$
Come ogni teorema, il teorema di Gauss va dimostrato. Dimostrarlo nel caso generale, tuttavia, è alquanto complicato. Ci apprestiamo dunque a dimostrarlo in due casi: quando la superficie $\mathcal{S}$ non racchiude alcuna carica, e quando la superficie $\mathcal{S}$ è una sfera, al centro della quale è posta un’unica carica puntiforme.
Caso 1
Supponiamo per semplicità che il campo elettrico a nostra disposizione, generato da una qualche distribuzione di cariche elettriche, sia uniforme, cioè sempre uguale in modulo, direzione e verso ad un certo vettore $\vec{E}$. Supponiamo altresì che la superficie $\mathcal{S}$ sia quella di un cubo, posto di modo che le linee di campo di $\vec{E}$ (che sono delle rette) siano perpendicolari a due facce opposte di $\mathcal{S}$. Con riferimento alla figura seguente, siano queste due facce i quadrati $ABCD$ ed $WXYZ$.
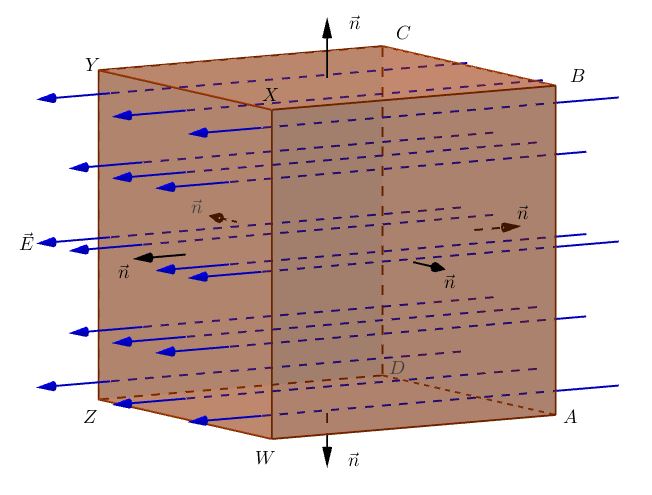
Osserviamo innanzitutto che, per come è posto il cubo all’interno delle linee di campo, esse formano un angolo retto con il versore normale alle facce “laterali” $BCYX$, $CDZY$, $ADZW$ e $ABXW$: attraverso queste facce, il flusso è nullo, essendo il campo vettoriale radente alla superficie.
Sempre con riferimento alla figura precedente, attraverso la faccia $ABCD$ il flusso sarà $\Phi_{ABCD} (\vec{E}) = S E \cos(180^\circ) = -S E$, essendo $S$ l’area del quadrato $ABCD$. In modo analogo, il flusso attraverso $WXYZ$ si può calcolare come $\Phi_{WXYZ} (\vec{E}) = S E \cos(0^\circ) = S E$. Allora il flusso totale è nullo: infatti,$$ \Phi_{\mathcal{S}} (\vec{E}) = \Phi_{ABCD} (\vec{E}) + \Phi_{WXYZ} (\vec{E}) = -ES + ES = 0 $$Ora proseguiamo nel ragionamento, ponendo, all’interno del campo uniforme $\vec{E}$ una superficie chiusa di forma qualunque. Possiamo riempire questo volume con dei cubi, approssimandone la forma: la precisione di questa approssimazione dipende dal numero e dalla dimensione dei cubi considerati; con un po’ di immaginazione, possiamo rendere arbitrariamente precisa questa approssimazione, aumentando all’infinito il numero di cubi e riducendone la dimensione a un volume minuscolo: al limite, questi infiniti cubi di volume infinitesimo costituiranno l’intero volume racchiuso dalla superficie $\mathcal{S}$.
Il flusso del campo elettrico uscente da $\mathcal{S}$ si può calcolare sommando i vari flussi che otteniamo facendo attraversare alle linee di campo i cubi usati per approssimare il volume racchiuso da $\mathcal{S}$: ma il flusso attraverso ciascuno di questi cubi è nullo, dunque il flusso totale è anch’esso pari a zero.
Il ragionamento appena fatto è ben lungi da una dimostrazione rigorosa, ma fornisce l’idea con la quale il calcolo svolto per un singolo cubo può essere generalizzato a una superficie qualsiasi.
Un’ulteriore generalizzazione può essere fatta rimuovendo anche l’ipotesi che il campo $\vec{E}$ sia uniforme. In conclusione, possiamo asserire che, se una superficie $\mathcal{S}$ non racchiude nessuna carica (ossia se la carica interna ad $\mathcal{S}$ è $q = 0$), il flusso uscente da $\mathcal{S}$ del campo elettrico $\vec{E}$, qualunque esso sia, è nullo: questo risultato si ottiene dal teorema di Gauss, ponendo $q = 0$.
Caso 2
Abbiamo ora a disposizione una singola carica puntiforme $q$ posta al centro di una sfera $\mathcal{S}$ di raggio $R$. Il risultato previsto in questo caso dal teorema di Gauss è $\Phi_{\mathcal{S}} (\vec{E}_q) = \frac{q}{\varepsilon}$: vediamo di ottenerlo mediante un calcolo diretto del flusso.
L’espressione del campo elettrostatico generata da $q$, su un punto della sfera (posto quindi a distanza $R$ da essa), è $$ \vec{E}_q (R) = \frac{1}{4 \pi \varepsilon} \cdot \frac{q}{R^2} \vec{u}_r $$La direzione di $\vec{u}_r$ punta da $q$, posto al centro della sfera, ad un punto sulla superficie sferica: è posto quindi su una direzione individuata da un raggio, con verso uscente dalla sfera, come illustrato in figura.

Come si può ben vedere dall’illustrazione, il versore normale uscente dalla superficie, $\vec{n}$, è parallelo al campo elettrico su un punto della superficie; concorde nel caso di una carica positiva $q > 0$ ($\alpha = 0^\circ$), discorde nel caso di una carica negativa $ q < 0 $ ($\alpha = 180^\circ$). Questo accade in ogni punto della superficie sferica.
Ricordando che la superficie della sfera è data dalla formula $S = 4 \pi R^2 $, il flusso del campo elettrico generato da $q$ uscente dalla sfera è pari a $$ \Phi_{\mathcal{S}} (\vec{E}_q) = \frac{1}{4 \pi \varepsilon} \cdot \frac{q}{R^2} 4 \pi R^2 = \frac{q}{\varepsilon} $$Anche in questo caso il teorema di Gauss risulta dimostrato.
Caso Generale
Il caso generale è alquanto complicato da dimostrare. Basti sapere che il caso appena dimostrato si può generalizzare a una superficie chiusa $\mathcal{S}$ di forma qualsiasi, e ad una qualunque disposizione di cariche. Si giunge al risultato $$ \Phi_{\mathcal{S}} (\vec{E}) = \frac{\sum q_{\text{int}}}{\varepsilon} $$dove $\sum q_{\text{int}}$ indica la carica totale racchiusa dalla superficie $\mathcal{S}$.
È importante far notare la generalità del risultato: esso non dipende né dalla forma della superficie, ma solo dal fatto che essa sia chiusa, né dalla presenza di cariche esterne alla superficie, né dalla disposizione specifica delle cariche interne ad essa.
È altresì possibile dimostrare che questo risultato è essenzialmente dovuto all’espressione analitica del campo elettrico, derivante dalla legge di Coulomb: il campo elettrico è un campo radiale (dipende solo dalla distanza dalle cariche generatrici, ed è orientato come il raggio di una sfera con centro la carica generatrice) ed il suo modulo è inversamente proporzionale al quadrato della distanza (infatti presenta un termine $\frac{1}{r^2}$). Per un qualunque campo dotato di queste caratteristiche, si può dimostrare un analogo del teorema di Gauss. Ma c’è di più: assumendo come postulato il teorema di Gauss, e seguendo la sua dimostrazione al contrario, si può dimostrare che la forza di Coulomb ha proprio l’espressione $ \vec{F} = \frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2} $. Si tratta quindi di una caratteristica fondamentale del campo elettrico, che ne cattura l’essenza. In effetti, assieme alla circuitazione, il flusso di un campo vettoriale ne descrive completamente il comportamento: le equazioni di Maxwell per il campo elettrico sono equivalenti al teorema di Gauss unitamente al fatto che la circuitazione del campo elettrostatico è nulla.
Mostriamo ora un’applicazione del teorema di Gauss: ci proponiamo di calcolare l’intensità del campo elettrico presente tra le armature di un condensatore.
Un condensatore è un dispositivo che si usa prevalentemente per accumulare carica elettrica. Nella sua versione più semplice, detto condensatore piano, esso è costituito da due piastre di materiale conduttore, dette armature, su cui è distribuita una certa carica elettrica $Q$, positiva su una armatura e negativa sull’altra, poste ad una certa distanza fra loro. Supponiamo che le armature abbiano area $S$, e definiamo la densità superficiale di carica $\sigma$ come il rapporto tra la carica disponibile $Q$ e l’area $S$ su cui è distribuita: $$ \sigma = \frac{Q}{S} $$

Il campo elettrico presente all’interno delle due armature è uniforme (in realtà non lo è: più ci si avvicina al bordo delle armature, più la forma delle linee di campo devia dalla retta; questi effetti, detti effetti di bordo, sono trascurabili ai fini di questa trattazione). Sia dunque $\vec{E}$ il campo elettrico entro il condensatore, diretto come delle rette perpendicolari alle armature e avente verso che punta dalla piastra con carica positiva a quella con carica negativa. Calcoleremo l’intensità di $\vec{E}$, cioè il suo modulo, con un ingegnoso utilizzo del teorema di Gauss.
Occorre però precisare una proprietà fondamentale dei materiali conduttori: il campo elettrico all’interno di un materiale conduttore è nullo (così come la carica contenuta all'interno di un conduttore, la quale si addensa sulla sua superficie). Come diretta conseguenza, le linee del campo elettrico sono sempre perpendicolari alla superficie di un conduttore.
Ciò detto, scegliamo come superficie chiusa un cilindro $\mathcal{C}$ posto a metà all’interno di una delle due armature del condensatore, con asse parallelo alle linee di campo, così come illustrato in figura:

Indichiamo con $L$ la superficie laterale del cilindro, con $S$ l’area delle basi del cilindro, e ci riferiremo con $\mathcal{S}_{\text{int}}$ alla base del cilindro interna al conduttore e con $\mathcal{S}_{\text{ext}}$ alla base del cilindro posta tra le due armature.
Applicando la definizione di flusso, sappiamo che il flusso uscente dalla superficie laterale $L$ è nullo, in quanto le linee di campo sono radenti a tale superficie. Per quanto riguarda la base $\mathcal{S}_{\text{int}}$, non venendo attraversata da alcuna linea di campo (per quanto appena detto sui materiali conduttori), il flusso sarà anche in questo caso nullo; infine, il flusso del campo elettrico uscente da $\mathcal{S}_{\text{ext}}$, essendo questa volta le linee di campo ortogonali ad essa, sarà $\Phi_{\mathcal{S}_{\text{ext}}} (\vec{E}) = E S $. Questo valore rappresenta il flusso totale del campo elettrico uscente dal cilindro $\mathcal{C}$, essendo nulli i contributi attraverso le altre superfici: possiamo quindi scrivere $$ \Phi_{\mathcal{C}} (\vec{E}) = E S $$D’altra parte, applicando il teorema di Gauss al caso in esame, sappiamo che $\Phi_{\mathcal{C}} (\vec{E}) = \frac{q}{\varepsilon}$, dove la carica $q$ è quella racchiusa entro la superficie del cilindro $\mathcal{C}$. Questa carica si può calcolare sfruttando la densità superficiale di carica $\sigma$: avendo a disposizione un’area $S$, la carica racchiusa all’interno del cilindro $\mathcal{C}$ è pari a $$ q = \sigma S $$Sostituendo questa relazione nell’espressione ottenuta dal teorema di Gauss, otteniamo $$\Phi_{\mathcal{C}} (\vec{E}) = \frac{\sigma \ S}{\varepsilon}$$Uguagliando le due espressioni trovate per il flusso otteniamo l’equazione $$ E \ S = \frac{\sigma \ S}{\varepsilon}$$che, semplificando per $S$, ci permette di ottenere l’espressione del campo elettrico all’interno delle armature di un condensatore piano: $$ E = \frac{\sigma}{\varepsilon} $$