Le derivate parziali di una funzione di più variabili possono essere considerate a tutti gli effetti come delle funzioni a più variabili. Nulla ci vieta quindi di derivarle a loro volta rispetto a una qualsiasi variabile tra quelle utilizzate per definire la funzione di partenza.
Definizione
Consideriamo una funzione di più variabili $f: \mathbb{R}^n \rightarrow \mathbb{R}$ e una sua derivata parziale $\frac{\partial f}{\partial x_i}$, con $1 \leq i \leq n$. Una derivata parziale di questa derivata, che indichiamo con $$\frac{\partial^2 f}{\partial x_j\partial x_i}, \qquad 1 \leq j \leq n $$è detta derivata parziale seconda o più semplicemente derivata seconda di $f$ rispetto alle variabili $x_i$ e $x_j$. Inoltre se $i = j$ la derivata seconda è detta pura, e si indicherà con $frac{\partial^2 f}{\partial x_i^2}$, mentre se $i \neq j$ si parla di derivata seconda mista.
Ci sono alcune cose importanti da dire prima di procedere ulteriormente.
- Nessuno ci assicura che le derivate seconde esistano (sono pur sempre limiti!).
- Se disponiamo di un’espressione analitica per le derivate parziali, le derivate seconde si calcolano esattamente con la stessa regola che si usa per determinare le derivate parziali (cioè derivando “ignorando” le variabili rispetto alle quali non stiamo derivando).
In molti altri casi, però, bisognerà ricorrere alla definizione di derivata e quindi al calcolo di un limite di più variabili. - L’ordine delle variabili rispetto alle quali deriviamo $f$ è, in generale, estremamente rilevante. Si consideri ad esempio la funzione $$f(x, y) = x^2y^{\frac{1}{3}}$$di cui vogliamo calcolare le derivate seconde miste nell’origine. Le derivate parziali di $f$ sono ##KATEX##\begin{aligned} \frac{\partial f}{\partial x} & = 2xy^{\frac{1}{3}} \\ \frac{\partial f}{\partial y} & = \frac{1}{3}x^2y^{-\frac{2}{3}} \end{aligned}##KATEX##Ci si accorge subito che non ha senso calcolare la derivata seconda $\frac{\partial^2 f}{\partial x \partial y}$ nell’origine, dato che persino la derivata parziale rispetto a $y$ non è definita in $(0,0)$. Invece, usando proprio la definizione di derivata parziale, otteniamo:$$\frac{\partial^2 f}{\partial y \partial x}(O) = \lim_{h \to 0} \frac{\frac{\partial f}{\partial x}(0,h) - \frac{\partial f}{\partial x}(0,0)}{h} = 0$$Quindi in questo caso la derivata seconda mista $\frac{\partial^2 f}{\partial x \partial y}$ non esiste, mentre l’altra esiste e vale $0$.
Per fortuna ci sono situazioni in cui possiamo non farci troppi problemi, come mostrato dal seguente teorema.
TEOREMA (di Schwarz). Consideriamo una funzione $f: \mathbb{R}^n \rightarrow \mathbb{R}$ per cui siano definite tutte le derivate seconde. Se le derivate miste sono anche continue, allora vale $$\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i} \qquad 1 \leq i,j \leq n, \ i \neq j$$In altre parole: se le derivate seconde miste esistono e sono continue, allora l’ordine di derivazione è irrilevante.
Definizione
La matrice quadrata che contiene le derivate seconde di una funzione di più variabili $f$ è detta matrice Hessiana di $f$, e la indichiamo con $\text{H} f$. In particolare, l’elemento alla riga $i$ e alla colonna $j$ è la derivata $\frac{\partial^2 f}{\partial x_i \partial x_j}$: otteniamo quindi $$\text{H} f:= \left ( \begin{matrix} \frac{\partial^2 f}{\partial x_1 \partial x_1} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n \partial x_n} \end{matrix} \right )$$Inoltre:
- il determinante di $\text{H} f$ è detto Hessiano di $f$;
- la traccia di $\text{H} f$ è detta Laplaciano di $f$ e lo indicheremo così: $$\Delta f = \frac{\partial^2 f}{\partial x_1 \partial x_1} + \frac{\partial^2 f}{\partial x_2 \partial x_2} + \ldots + \frac{\partial^2 f}{\partial x_n \partial x_n}$$
Vale la pena di notare che la matrice Hessiana di una funzione che rispetta le ipotesi del teorema di Schwarz è simmetrica.
Massimi e minimi per funzioni di due variabili
In questo paragrafo vogliamo spiegare come determinare massimi e minimi (locali) di una funzione $f: \mathbb{R}^2 \rightarrow \mathbb{R}$ differenziabile e per cui siano definite le derivate seconde. Questo procedimento farà uso della matrice Hessiana, strumento che abbiamo appena introdotto.
Con massimo (globale) di $f$ intendiamo un valore $M$ tale per cui $f(x) \leq M \ \forall x \in \mathbb{R}^2$; il massimo sarà locale se la condizione $f(x) \leq M$ è valida solo in un intorno del punto di massimo, che è quel punto $x_0 \in \mathbb{R}^2$ tale per cui $f(x_0)=M$. Le definizioni di minimo, minimo locale e punto di minimo sono del tutto analoghe.
Per visualizzare i massimi e minimi di $f$ possiamo dire che, intuitivamente, stiamo parlando di punti per cui il grafico di $f$, nelle “vicinanze”, sembra una “collina” o una “scodella”, rispettivamente:

Si può intuire quindi che nei punti di massimo o di minimo la funzione non cresce e non decresce rispetto a tutte le direzioni che possiamo percorrere: stiamo cioè dicendo che tutte le derivate direzionali devono essere nulle. Questa condizione non è sempre molto agevole da verificare; tuttavia, grazie al teorema del gradiente, possiamo permetterci di controllare che solamente le derivate parziali siano nulle, dato che le altre derivate direzionali si ottengono come combinazioni lineari delle derivate parziali. Riassumendo, abbiamo ottenuto una condizione necessaria affinché un punto di $\mathbb{R}^2$ sia di massimo o di minimo: il gradiente di $f$ deve essere il vettore nullo. Siamo quindi a conoscenza di uno strumento per individuare i candidati a punti di massimo e di minimo per una funzione di due variabili, che ci ricorda la condizione necessaria nel caso di funzioni di una variabile (il teorema di Fermat).
Definizione
Un punto $P \in \mathbb{R}^2$ per cui $\nabla f(P) = (0,0)$ è detto punto stazionario.
Un punto di massimo o di minimo sarà quindi necessariamente un punto stazionario; non tutti i punti stazionari però sono di minimo o di massimo. Per esempio, prendiamo la funzione $f(x,y)=xy$: si verifica facilmente che entrambe le derivate parziali sono nulle nell’origine $O$, ma di certo la funzione può assumere valori ben più grandi e ben più piccoli di $f(O)=0$.

Definizione
Un punto stazionario per $f$ che non sia né un punto di massimo né un punto di minimo è detto punto di sella. (Il nome che abbiamo appena dato viene giustificato dalla forma che il grafico della funzione assume in corrispondenza del punto considerato.)
Come facciamo a distinguere tra massimi, minimi e selle?
TEOREMA. Consideriamo l’Hessiano $\text{det} \left ( \text{H}f \right )$ e il Laplaciano $\Delta f$ di $f$, e un punto stazionario $P$.
- Se $\text{det} \left ( \text{H}f(P) \right ) < 0$, allora il punto è di sella.
- Se $\text{det} \left ( \text{H}f(P) \right ) > 0$ e $\Delta f(P) > 0$, allora il punto è di minimo (locale o eventualmente globale).
- Se $\text{det} \left ( \text{H}f(P) \right ) > 0$ e $\Delta f(P) < 0$, allora il punto è di massimo (locale o eventualmente globale).
Il teorema non parla di cosa succede quando $\text{det} \left ( \text{H}f \right ) = 0$. In effetti non esiste un metodo generale per capire cosa succede in una situazione del genere: bisogna procedere utilizzando qualche trucco ad hoc che ci permetta di capire come si comporta la funzione considerata.
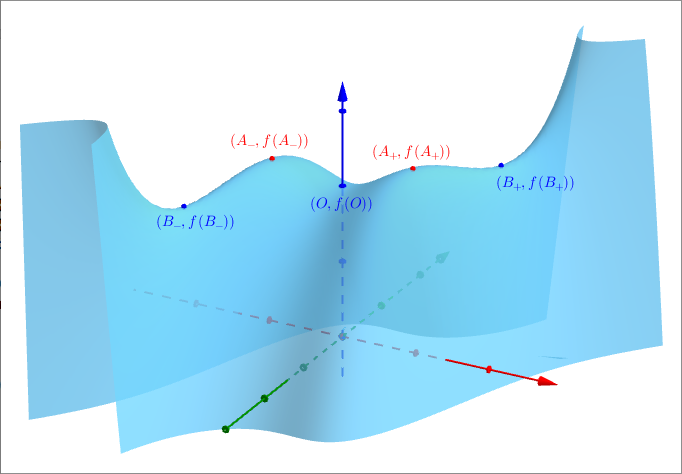
Svolgiamo un esercizio utilizzando il teorema appena visto. Consideriamo la funzione $$f(x,y) = x^3y+x^2-y^2-x^4+2$$Questa funzione è differenziabile, e ha derivate parziali ##KATEX##\begin{aligned} \frac{\partial f}{\partial x} & = 3x^2y + 2x - 4x^3 = x(3xy + 2 - 4x^2) \\ \frac{\partial f}{\partial y} & = x^3 - 2y \end{aligned}##KATEX##Cerchiamo i punti stazionari, cioè i punti di $\mathbb{R}^2$ che annullano contemporaneamente entrambe le derivate parziali. Otteniamo $$\frac{\partial f}{\partial y} = 0 \quad \Leftrightarrow \quad y = \frac{x^3}{2}$$A partire da questa uguaglianza e imponendo anche $\frac{\partial f}{\partial x} = 0$ si ha$$\nabla f = (0,0) \quad \Leftrightarrow \quad x \left ( \frac{3x^4}{2} + 2 - 4x^2 \right ) \ \wedge \ y = \frac{x^3}{2}$$La prima condizione è soddisfatta quando $x=0$ oppure quando $\frac{3x^4}{2} + 2 - 4x^2 = 0$, che è una equazione biquadratica con soluzioni $x = \pm \sqrt{\frac{2}{3}}$ e $x = \pm \sqrt{2}$. Utilizzando la seconda condizione otteniamo i seguenti punti stazionari: $$A_{\pm} \equiv \left ( \pm \sqrt{\frac{2}{3}}, \pm \frac{1}{3} \sqrt{\frac{2}{3}} \right ) , \quad B_{\pm} \equiv \left ( \pm \sqrt{2}, \pm \sqrt{2} \right ), \quad O \equiv (0,0)$$Vogliamo capire se questi punti sono di massimo, di minimo o di sella per $f$. Per farlo calcoliamo la matrice Hessiana di $f$: $$\text{H} f = \left ( \begin{matrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} \end{matrix} \right ) = \left ( \begin{matrix} 6xy+2-12x^3 & 3x^2 \\ 3x^2 & -2 \end{matrix} \right )$$A questo punto sostituiamo ciascun punto stazionario nell’Hessiana per vedere che tipo di punti sono:##KATEX##\begin{aligned} \text{H} f \left ( A_{\pm} \right ) & = \left ( \begin{matrix} -\frac{14}{3} & 2 \\ 2 & -2 \end{matrix}##KATEX## \right ) \\ \text{H} f \left ( B_{\pm} \right ) & = \left ( ##KATEX##\begin{matrix} -10 & 6 \\ 6 & -2 \end{matrix}##KATEX## \right ) \\ \text{H} f \left ( O \right ) & = \left ( ##KATEX##\begin{matrix} 2 & 0 \\ 0 & -2 \end{matrix}##KATEX## \right ) \end{aligned}
Quindi:##KATEX##\begin{aligned} \text{det} \left ( \text{H}f \left ( A_{\pm} \right ) \right ) & = \frac{16}{3} > 0 \qquad \Delta f(A_{\pm}) = - \frac{20}{3} < 0 \\ \text{det} \left ( \text{H}f \left ( B_{\pm} \right ) \right ) & = -16 < 0 \\ \text{det} \left ( \text{H}f(O) \right ) & = -4 < 0 \end{aligned}##KATEX##Dall’enunciato del teorema otteniamo quindi che:
- i punti $A_{\pm}$ sono entrambi di massimo;
- i punti $B_{\pm}$ sono entrambi di sella;
- il punto $O$ è anch’esso di sella.
Il massimo assunto da $f$ in $A_{\pm}$ è locale, dato che $f \left ( A_{\pm} \right ) = \frac{62}{27} \approx 2,3$ ma, per esempio, $f(2,3) = 5$.
Attezione, però: quando l'insieme su cui stiamo cercando massimi e minimi non è l'intero dominio della funzione ma è, per esempio, il supporto di una curva nel piano, si deve ricorrere ad altri metodi: uno dei più utili e comodi è il cosiddetto metodo dei moltiplicatori di Lagrange.