Problema
Nella figura 1 è rappresentato il grafico $\Gamma$ della funzione continua $f : [0, +\infty) \rightarrow \mathbb{R}$, derivabile in $(0,+\infty)$, e sono indicate le coordinate di alcuni suoi punti.

È noto che $\Gamma$ è tangente all’asse $y$ in $A$, che $B$ ed $E$ sono un punto di massimo ed uno di minimo, che $C$ è un punto di flesso con tangente di equazione $2x + y - 8 = 0$.
Nel punto $D$ la retta tangente ha equazione $x + 2y -5 = 0$ e per $ x \geq 8$ il grafico consiste di una semiretta passante per il punto $G$. Si sa inoltre che l’area della regione delimitata dall’arco $ABCD$, dall’asse $x$ e dall’asse $y$ vale $11$, metre l’area della regione delimitata dall’arco $DEF$ e dall’asse $x$ vale $1$.
- In base alle informazioni disponibili, rappresenta indicativamente i grafici delle funzioni$$ \begin{array}{c} y = f’(x) \\ F(x) = \int_0^x f(t) dt \end{array}$$Quali sono i valori di $f’(3)$ e $f’(5)$? Motiva la tua risposta.
- Rappresenta indicativamente i grafici delle seguenti funzioni:$$ \begin{array}{c} y = |f’(x)| \\ y = |f(x)|’ \\ y = \frac{1}{f(x)} \end{array}$$specificando per ciascuna di esse l’insieme di definizione.
- Determina i valori medi di $y = f(x)$ e $y = | f(x) |$ nell’intervallo $[0,8]$, il valore medio di $y = f’(x)$ nell’intervallo $[1,7]$ e il valore medio di $y = F(x)$ nell’intervallo $[9,10]$.
- Scrivi le equazioni delle rette tangenti al grafico della funzione $F(x)$ nei suoi punti di ascisse $0$ e $8$, motivando le risposte.
Soluzione
1. Iniziamo col tracciare un grafico approssimativo della funzione$$ F(x) = \int_{0}^{x} f(t) dt $$Si tratta della funzione integrale di $f$, che, per il teorema di Torricelli, è una primitiva di $f$. Dalle informazioni in nostro possesso, possiamo subito dire che:
- $F(0) = 0$, in quanto $\int_0^0 f(t) dt = 0$.
- $F(5) = 11$. Questo segue dal fatto che l’area sottesa all’arco $ABCD$ e compresa nel primo quadrante vale proprio $11$. Sull’intervallo $[0,5]$ la funzione $f$ è non negativa, come si evince dal grafico, e quindi il valore di quest’area, $11$, è proprio $\int_0^5 f(t) dt$, ossia $F(5)$.
- $F(8) = 10$. Sappiamo che l’area compresa tra l’asse $x$ e l’arco $DEF$ vale $1$. Nell’intervallo $[5, 8]$, tuttavia, $f$ non assume valori positivi: per la definizione dell’integrale di Riemann, avremo $ 1 = - \int_5^8 f(t) dt $. Per le proprietà dell’integrale, possiamo dire che $ F(8) = \int_0^8 f(t)dt = \int_0^5 f(t)dt + \int_5^8 f(t)dt$. Di conseguenza,$$ F(8) = F(5) + \int_5^8 f(t)dt = F(5) -1 = 10$$
- Tra $x = 1$ ed $x = 5$ $F$ è crescente, così per $x \geq 8$; per $x$ compreso tra $5$ ed $8$, invece, $F$ è decrescente. Questo si deduce dall’anasili del segno di $f$.
- In $x = 1$ e $x = 7$, il grafico di $F$ presenterà dei flessi. Questo perchè $f$ ammette, in in corrispondenza di quei valori di $x$, punti di massimo o minimo, e quindi $f’(x)$, che altri non è che $F’’(x)$, ammetterà degli zeri. Non sappiamo il valore di $F(1)$ o $F(7)$.
- Da $8$ in poi, sappiamo che il grafico di $f$ è costituito da una semiretta, passante per i punti $G$ ed $F$. Siccome la funzione $F$ è una primitiva di $f$, se riusciamo ad ottenere l’espressione analitica di $f$ mediante un integrale potremo ottenere quella di $F$. Questo è abbastanza facile, basta calcolare la retta passante per i due punti: si trova, dopo semplici calcoli, che la retta in questione è $ y = 2x - 16 $. Una primitiva di questa funzione è $ x^2 - 16x + c $, con $c$ costante arbitraria.
Dobbiamo naturalmente determinare il valore di $c$: imponiamo che il valore di $ x^2 - 16x + c $ per $x = 8$ coincida con il valore che già conosciamo per $F$ nel punto $x=8$, cioè $F(8) = 11$: giungiamo allora all’equazione $ 11 = 8^2 - 16 \cdot 8 + c \ \Rightarrow \ c = 74 $.
Il grafico della funzione integrale $F$ quindi, dopo $8$, assumerà la forma della parabola di equazione $ y = x^2 - 16x + 74$. Notiamo che, siccome è richiesto solo un disegno, non è necessario scrivere questa espressione: è sufficiente indicare che, per $ x \geq 8 $, il grafico di $F$ è una parabola che passa da $(8 ;10)$. Il calcolo di quest’espressione però sarà utile per il seguito.
Mettendo assieme tutte queste informazioni, un grafico approssimativo potrebbe essere il seguente:

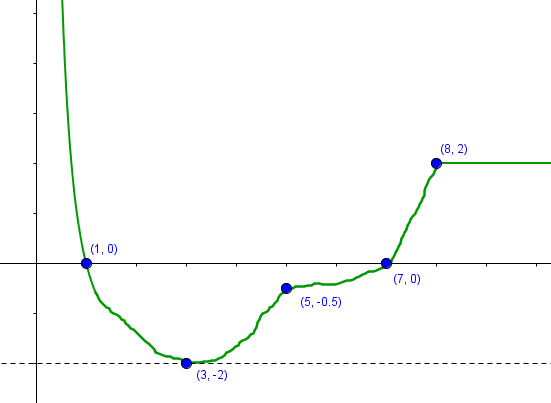
Per quanto riguarda il grafico di $f’(x)$, invece, prendiamo in considerazione i seguenti fatti:
- La funzione $f$ presenta un massimo in $x=1$ e un minimo in $x=7$, ed è ivi derivabile. Ne deduciamo quindi, per il teorema di Fermat, che $f’(1) = f’(7) = 0$.
- Sappiamo anche che $f$ è crescente da $0$ a $1$, decrescente da $1$ a $7$, e poi di nuovo crescente sino ad $\infty$. Il grafico di $f’$ sarà quindi sopra l’asse delle $x$ tra $0$ e $1$ e dopo $7$, mentre si trova sotto l’asse delle ascisse tra $1$ e $7$, in quanto lo studio della monotonia di $f$ determina il segno di $f’$.
- In $x=3$ $f$ presenta un punto di flesso (non verticale); di conseguenza, $f’$ avrà un punto a tangente orizzontale, dato che la sua derivata, $f’’$, vale zero in quel punto.
- Continuando l’analisi sulla convessità di $f$, vediamo che questa è convessa tra $0$ e $3$ (fino al flesso), concava da $3$ in poi. $f’$ di conseguenza sarà non crescente (o decrescente in senso lato) sino a $3$ e, in seguito, non decrescente (o crescente in senso lato).
- Da $x=8$ in poi, $f$ è una retta. Precisamente, come abbiamo calcolato in precedenza, la retta $ y = 2x - 16 $. Di conseguenza, $f’$, per $x \geq 8$, vale costantemente $2$.
- Il testo fornisce le espressioni delle rette tangenti al grafico di $f$ nei punti di ascisse $3$ e $5$. Ricordiamo che il valore della derivata di $f$, in quei punti, rappresenta il coefficiente angolare di tali rette. Quest’ultime sono però date in forma implicita: basta svolgere semplici calcoli algebrici per trovare anche le loro forme esplicite:$$ \begin{array}{l} 2x + y -8 = 0 \Rightarrow y = -2 x + 8 \\ x + 2y - 5 = 0 \Rightarrow y = -\frac{1}{2} x + \frac{5}{2} \end{array}$$Di conseguenza, abbiamo che $f’(3) = -2$ e $f’(5) = - \frac{1}{2} $. Questo risponde a due richieste: quella in calce alla consegna di disegnare i grafici, e aggiunge inoltre che il grafico di $f’$ deve passare dai punto $(3; -2)$ e $\left(5; -\frac{1}{2}\right)$.
- Infine, il grafico di $f$ tocca l’asse $y$, in $x=0$, con tangente verticale: di conseguenza, $f’(x)$ deve tendere all’infinito per $x \to 0^-$. Dalle considerazioni già fatte sul segno di $f’$, questo non può che essere $+ \infty$.
Con tutte queste informazioni possiamo apprestarci a disegnare un grafico approssimativo di $f’$:
2. Viene chiesto di tracciare i grafici di alcune funzioni che si possono dedurre, mediante semplici trasformazioni geometriche, da quello presentato in consegna o quelli disegnati al punto precedente.
Iniziamo con il grafico di $y = | f’(x) | $. Ricordiamo che, in generale, dato il grafico della funzione $y = h(x)$, il grafico di $ y = | h(x) |$ si ottiene “ribaltando” tutto quel tratto in cui $h$ è negativa al di sopra dell’asse delle ascisse. Nel nostro caso, avremo quindi che tutto il tratto di grafico da $x=1$ a $x=7$ deve essere riflesso sull’asse $x$:
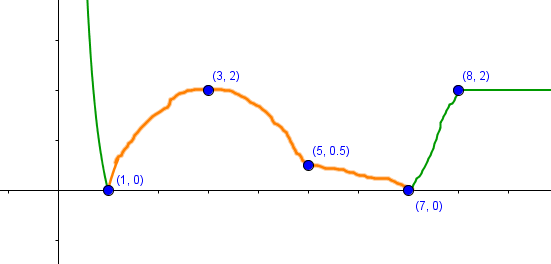
Abbiamo evidenziato in arancione la parte di grafico da modificare. Il dominio di $y = |f’(x)|$ è lo stesso di $f’(x)$: $(0, +\infty)$.
Per tracciare facilmente $y = | f(x) |’$, basta ricordarsi la definizione di valore assoluto e le proprietà della derivata. Abbiamo infatti che$$ | f(x) |’ = \begin{cases} f’(x) & \text{ se } f(x) > 0 \\ (-f(x))’ = -f’(x) & \text{ se } f(x) < 0 $ \end{cases}$$Nella seconda equazione abbiamo usato la linerità della derivata. Tracciare il grafico è semplice quindi: se $f(x) >0$ non cambia nulla; ovunque $f(x)$ risulti negativa, invece, ribalteremo il grafico di $f’$ rispetto all’asse delle ascisse: questo accade tra $5$ e $8$. Il risultato è, pressappoco, il seguente:

Il dominio di questa funzione è $(0,5) \cup (5,8) \cup (8, +\infty)$: $|f(x)|’$ non è definita in $5$ o $8$ perchè la funzione $|f(x)|$, in quei punti, non è derivabile.
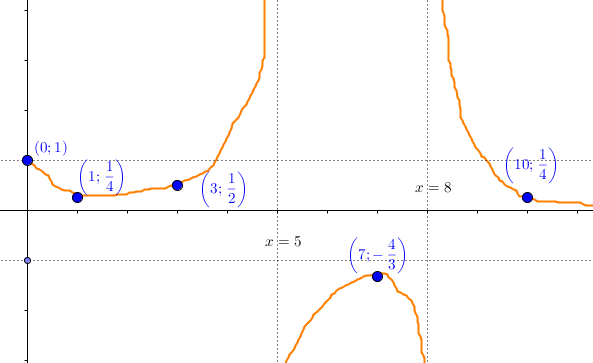
Il grafico di $y = \frac{1}{f(x)}$ si può tracciare facendo le seguenti considerazioni:
- $\frac{1}{1} = 1$, quindi dove $f$ vale $1$ anche $\frac{1}{f}$ deve valere $1$
- Nello stesso spirito, quando il grafico di $f$ supera l’ordinata $1$ il grafico di $\frac{1}{f}$ deve stare sotto l’ordinata $1$, e viceversa. Questo deriva dal fatto che $ z > 1 \ \Leftrightarrow \ \frac{1}{z} < 1 $, per ogni $z \neq 0$.
- Ovviamente, il segno di $f$ ed $\frac{1}{f}$ sono lo stesso.
- Ove il valore di $f$ si avvicina a $0$, $\frac{1}{f}$ deve tendere ad $\infty$: questo perchè $\lim_{z \to 0} \frac{1}{z} = \infty$. Analogamente, dato che $\lim_{z \to \infty} \frac{1}{z} = 0$, avremo che qualora $f$ tendesse all’infinito (come fa per $x \to +\infty$) il grafico di $\frac{1}{f}$ si dovrebbe avvicinare a $0$. Di conseguenza, avremo i seguenti limiti per $\frac{1}{f}$:$$ \begin{array}{l} \lim_{x \to 5^{\pm}} \frac{1}{f(x)} = \mp \infty \\ \lim_{x \to 8^{\pm}} \frac{1}{f(x)} = \pm \infty \\ \lim_{x \to + \infty} \frac{1}{f(x)} = 0 \end{array}$$Quindi avremo asintoti verticali in $x = 5$ ed $ x = 8 $, e un asintoto orizzontale per $x \to + \infty$ costituito dalla retta $y=0$.
- Il dominio di $y = \frac{1}{f(x)}$ si ottiene da quello di $f$ ponendo come condizione aggiuntiva che $f(x) \neq 0$: avremo quindi $[0,5) \cup (5,8) \cup (8,+\infty)$.
Tenuto conto di tutto questo, il grafico di $\frac{1}{f}$ dovrebbe assomigliare al seguente:
3. Ricordiamo innanzitutto, secondo la sua definizione, che il valor medio integrale di una funzione $h$ su di un intervallo chiuso e limitato $[a,b]$ è pari a$$ M = \frac{1}{ b - a } \int_{a}^{b} h (t) dt $$Detto questo, calcoliamo le medie richieste.
Per quanto riguarda la media di $f’$ su $[1,7]$, questa è presto detta. Sappiamo, per la definizione di primitiva, che $\int f’ = f $. Quindi avremo che $ \int_1^7 f’(x) dx = f(7) - f(1) = -\frac{3}{4} - 4 = - \frac{15}{4}$. Siccome $7 - 1 = 6$, la media richiesta vale $\frac{1}{6} \left( - \frac{15}{4} \right) = -\frac{15}{24} = - \frac{5}{8}$.
Per la funzione integrale $F$, abbiamo a disposizione un’espressione analitica calcolata nella risposta alla domanda 1: per $x \geq 8$ abbiamo infatti $F(x) = x^2 - 16x + 74$. L’intervallo su cui calcolare la media è ampio $1$ (infatti $10 - 9 = 1$) e quindi la media richiesta vale esattamente $ \int_{9}^{10} F(x) dx $. Questo è l’integrale di un polinomio, che si può svolgere seguendo semplici passaggi che derviano dalle prime proprietà dell’integrale. Abbiamo che $ \int_{9}^{10} F(x) dx = \int_{9}^{10} x^2 - 16x + 74 dx = \left[ \frac{1}{3} x^3 - 8 x^2 + 74x \right]_{9}^{10} = \frac{37}{3} $.
Infine, le medie di $f$ e $|f|$ si calcolano tenendo presente che $f$, tra $5$ ed $8$, assume valori negativi. Come abbiamo ricordato in precedenza, quindi, avremo che $ 1 = - \int_5^8 f(x) dx \Rightarrow \int_5^8 f(x) dx = - 1 $; d’altro canto, $|f|$ assume, per definizione, solo valori non negativi. Tenuto conto di tutto questo, possiamo dire che $\int_{0}^8 f(x) dx = \int_0^5 f(x) dx + \int_5^8 f(x) dx = 11 - 1 = 10$, mentre $\int_{0}^8 f(x) dx = 11 + 1 = 12$. In definitiva, la media di $f$ sull’intervallo prescelto vale $\frac{10}{8} = \frac{5}{4}$, mentre quella di $|f|$ vale $\frac{12}{8} = \frac{3}{2}$.
4. Per calcolare la retta tangete al grafico di $F$ in un dato punto $x$, occorre ricordare che questa retta è quella passante per il punto (del piano) $(x; F(x))$ e avente per coefficiente angolare la derivata $F’(x)$.
Sappiamo che, essendo $F$ funzione integrale di $f$, $F’(x) = f(x)$ ovunque ambo le espressioni abbiano senso.
In $x = 8$, quindi, la retta tangente al grafico di $F$ sarà quella passante per il punto $(8;10)$ e avente coefficiente angolare $f(8) = 0$: si tratta quindi della retta orizzontale$$y = 10 $$Per quanto riguarda $x = 0$, invece, sorge un problema: sebbene sia definita $f(0) = 1$, la funzione $F$ non è derivabile in $0$. Questo perchè non è possibile svolgere il limite del rapporto incrementale, necessario per calcolare la derivata $F’(0)$, in quanto a $0$ non è possibile avvicinarsi da sinistra, ma soltanto da destra.
Ad ogni modo, la tangente al grafico esiste eccome: è quella retta che passa per $(0;0)$ e ha, come coefficiente angolare, $f(0) =1$: si tratta quindi di$$ y = x $$Ricordiamo che, se una funzione $f$ è derivabile in un punto $x$, allora il suo grafico possiede una retta tangente nel punto $(x;f(x))$. Tuttavia, se il grafico di una funzione ammette una tangente in un certo punto non è detto che questa sia ivi derivabile: si consideri ad esempio un punto a tangente verticale.